La corrélation est un indicateur statistique qui mesure la force et le sens de la relation entre deux séries de données. Sa valeur varie entre –1 et +1 :
- +1 : indique l’existence d’une corrélation parfaitement positive (les deux variables évoluent dans le même sens).
- –1 : indique l’existence d’une corrélation parfaitement négative (elles évoluent en sens inverse).
- 0 : signifie qu’aucune relation linéaire significative n’existe entre les deux séries de données.
Cette fonction est particulièrement utile en finance, en économie ou en sciences sociales pour vérifier la dépendance entre deux variables (par exemple, l’évolution du chiffre d’affaires et des dépenses publicitaires ou le décryptage d’algorithmiques (SEO)). Elle vous permet d’explorer des champs de données importants, de les comprendre et d’établir des modèles d’explication. À titre personnel, je l’ai utilisé avec un certain succès pour modéliser en partie l’algorithme de Google.
Sommaire
Installer le pack Analysis ToolPak pour Excel
La fonction COEFFICIENT.CORRELATION n’est pas installée par défaut, mais est intégrée au pack Analysis ToolPak pour Excel. Il est normalement gratuit et pour en bénéficier, il vous faut l’installer comme un addon. La procédure peut varier selon la version d’Excel que vous possédez.
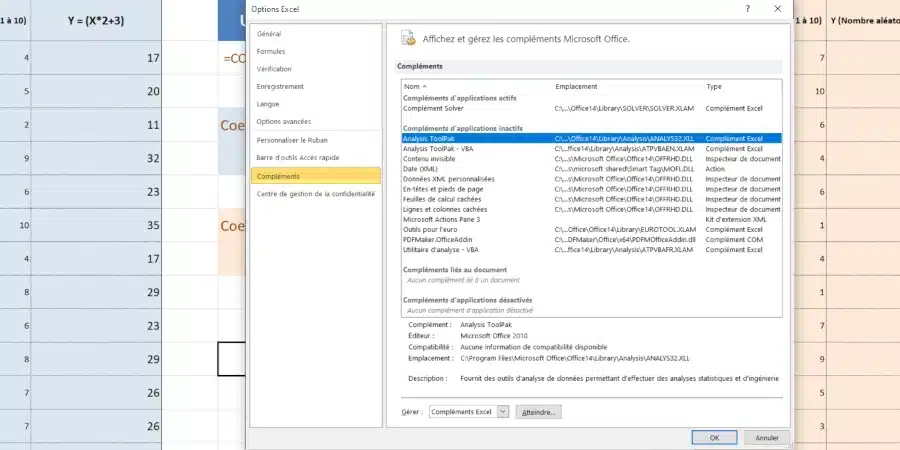
Pour en savoir plus, je vous invite à consulter la page suivante :
Load the Analysis ToolPak in Excel.
Les arguments de la fonction COEFFICIENT.CORRELATION()
=COEFFICIENT.CORRELATION(Matrice 1; Matrice 2)La fonction « COEFFICIENT.CORRELATION(Matrice 1; Matrice 2) » renvoie le coefficient de corrélation entre deux séries de données.
| Argument de la fonction | Signification de l’argument |
| Matrice 1 | 1ʳᵉ série de nombres |
| Matrice 2 | 2° série de nombres |
Important : Le nombre de cellules de la matrice 1 et de la matrice 2 doivent être identique, sinon cela génère une erreur.
Comment interpréter les résultats d’une corrélation ?
Lorsqu’on calcule un coefficient de corrélation, l’essentiel n’est pas seulement d’obtenir une valeur, mais de savoir ce qu’elle signifie concrètement. La corrélation mesure la force et le sens d’un lien entre deux variables numériques, avec un résultat compris entre –1 et +1.
Une valeur proche de +1 traduit une relation positive forte : lorsque la première variable augmente, la seconde a tendance à croître également. C’est le cas, par exemple, entre la taille et le poids dans une population donnée. À l’inverse, une valeur proche de –1 indique une relation négative forte : l’évolution d’une variable se fait en sens opposé à celle de l’autre, comme le nombre d’heures passées devant la télévision et les résultats scolaires dans certains échantillons.
Une valeur proche de 0 suggère qu’il n’existe pas de lien linéaire significatif entre les deux variables. Cela ne signifie pas forcément qu’il n’y a aucune relation, mais qu’elle n’est pas captée par ce type de mesure.
Il est également essentiel de garder en tête les limites de la corrélation : elle ne prouve jamais une causalité. Deux variables peuvent évoluer ensemble sans qu’il y ait de lien de cause à effet. Parfois, une troisième variable cachée explique cette association. Enfin, la présence de données extrêmes peut fausser le coefficient et donner une vision trompeuse de la réalité.
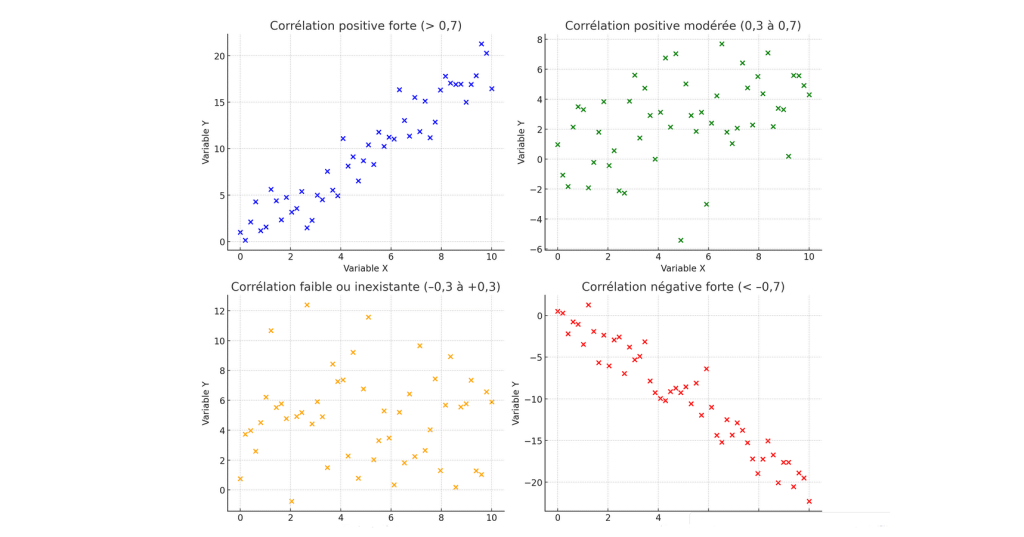
Corrélation > 0,7 : relation positive forte
Cela veut dire que lorsque la première variable augmente, la seconde augmente presque toujours en même temps et dans une proportion comparable.
Exemple : le nombre d’heures d’entraînement et la performance sportive. Plus on s’entraîne, meilleurs sont les résultats.
Corrélation entre 0,3 et 0,7 : relation positive modérée
Ici, la relation est réelle, mais pas parfaite : les deux variables évoluent dans le même sens, mais d’autres facteurs interviennent.
Exemple : le revenu et le niveau d’études. En général, plus le niveau d’études est élevé, plus le revenu augmente, mais ce n’est pas systématique.
Corrélation entre –0,3 et +0,3 : faible ou inexistante
Dans cette zone, la relation est trop faible pour être considérée comme significative. Les variables évoluent de manière indépendante.
Exemple : la pointure de chaussures et la réussite scolaire. Aucune relation logique, le coefficient sera proche de zéro.
Corrélation < –0,7 : relation négative forte
Cela signifie que lorsque la première variable augmente, la seconde diminue presque toujours. La relation est inverse et marquée.
Exemple : le prix d’un produit et la quantité demandée (loi de l’offre et de la demande). Plus le prix augmente, plus les ventes chutent fortement.
Conseils d’utilisation de la fonction Corrélation
- Le nombre de valeurs analysées doit suffisamment être important pour que le résultat soit significatif.
- Une corrélation forte ne prouve pas la causalité (deux variables peuvent être liées sans que l’une cause l’autre).
- La fonction corrélation ne mesure qu’une relation linéaire
- Des valeurs extrêmes peuvent fausser le résultat, d’où l’importance d’avoir des échantillons suffisamment importants pour diminuer le risque.
Vidéo : trader ou analyste ? Comprenez la fonction CORRÉLATION sous Excel en 5 minutes !
Foire aux questions (FAQ) la notion de corrélation et son mode de calcul avec Excel
Télécharger un exemple de tableau avec des coefficients de corrélation
Autres modèles de documents Excel
Votre avis et vos conseils sur l’utilisation de la fonction Corrélation sous Excel nous intéresse :
Dites-le-nous dans les commentaires. MERCI.








